散点图如何求方程
在数据分析和图形表示领域,散点图是一种非常常用的工具。它能够直观地展现两个变量之间的关系,帮助研究人员更好地理解数据的内在规律。当我们想要从散点图中提取出更深层次的信息时,就需要对散点图进行深入的分析,并尝试找出其中隐藏的数学模型。如何通过散点图来求解一个具体的数学方程呢?本文将为大家详细阐述这一过程。
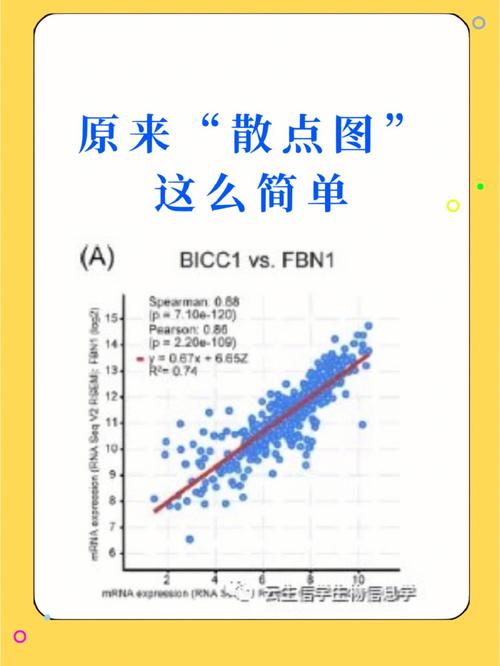
我们需要了解散点图的基本概念。散点图是一种二维图形,由两个坐标轴和一个或多个散点组成。每个散点代表一个观测值,其位置取决于该观测值对应的两个变量的值。通过观察散点在坐标轴上的位置和分布,我们可以初步判断两个变量之间是否存在某种关系。
接下来,我们可以尝试通过散点图来求解一个具体的数学方程。这通常需要以下几个步骤:
1. 观察散点图的分布特征:在散点图中,我们通常会注意到一些明显的规律性。例如,如果某个变量的值随着另一个变量的增加而增加或减少,那么我们可以尝试构建一个线性方程来描述它们之间的关系。反之,如果两个变量之间存在非线性关系,那么我们可能需要构建一个更复杂的多项式方程或其他类型的函数来描述它们的关系。
2. 确定自变量和因变量:在求解数学方程时,我们需要明确哪些变量是自变量,哪些变量是因变量。自变量通常是影响因变量变化的因素,而因变量则是受到自变量影响的量。在散点图中,我们可以通过观察散点的位置和大小来判断它们之间的相对重要性。
3. 选择合适的数学模型:根据自变量和因变量的特征,我们可以选择适合的数学模型来描述它们之间的关系。常见的数学模型包括线性方程、二次方程、指数方程、对数方程等。这些模型可以根据实际情况进行调整和优化,以便更准确地拟合散点图数据。
4. 求解数学方程:一旦我们确定了合适的数学模型,就可以使用相应的方法来求解这个方程。对于线性方程,我们可以使用最小二乘法等优化方法来找到最佳拟合参数。对于非线性方程,我们可能需要借助数值计算方法或图形化软件来求解。
5. 验证求解结果:为了确保我们的求解结果是正确的,我们需要对求解过程进行验证。这可以通过绘制原始数据与拟合曲线的对比图来实现。如果拟合曲线能够很好地反映原始数据的趋势和特点,那么我们就可以认为求解结果是可靠的。
6. 分析求解结果的意义:我们需要对求解结果进行深入分析,以了解它们对实际问题的意义。这可能涉及到对模型的解释、预测能力的评估以及对实际应用的影响等方面。通过这样的分析过程,我们可以更好地理解求解结果的价值和意义。
总结而言,通过散点图来求解一个数学方程是一个既有趣又有挑战的过程。它不仅需要我们对散点图有深入的了解和认识,还需要我们具备一定的数学建模能力和计算技能。通过以上步骤的指导和实践,我们可以逐步掌握这一技能,并将其应用于实际问题的解决中。希望本文能够帮助您更好地理解和掌握散点图求解数学方程的方法和技巧。